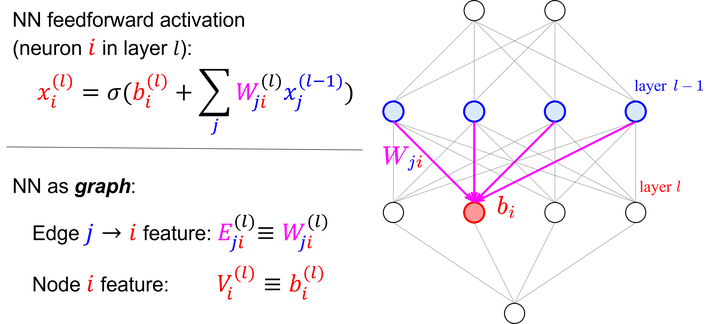
Neural Networks Are Graphs! Graph Neural Networks for Equivariant Processing of Neural Networks

Abstract

Neural networks that can process the parameters of other neural networks find applications in diverse domains, including processing implicit neural representations, domain adaptation of pretrained networks, generating neural network weights, and predicting generalization errors. However, existing approaches either overlook the inherent permutation symmetry in the weight space or rely on intricate weight-sharing patterns to achieve equivariance. In this work, we propose representing neural networks as computation graphs, enabling the use of standard graph neural networks to preserve permutation symmetry. We also introduce probe features computed from the forward pass of the input neural network. Our proposed solution improves over prior methods from 86% to 97% accuracy on the challenging MNIST INR classification benchmark, showcasing the effectiveness of our approach.