Roto-translated Local Coordinate Frames For Interacting Dynamical Systems
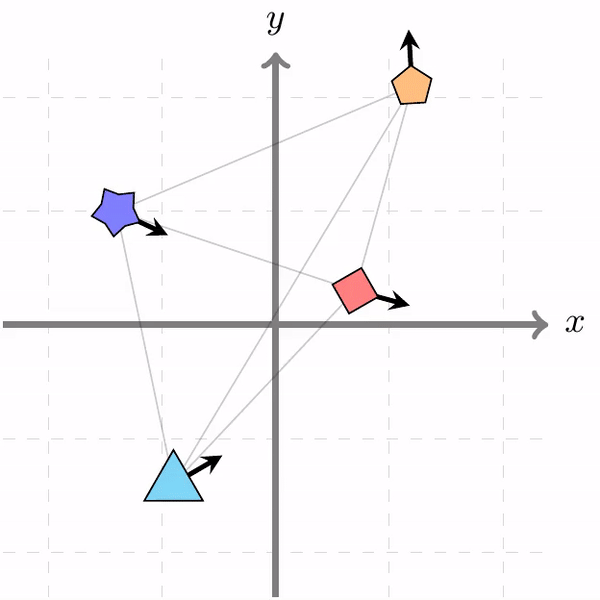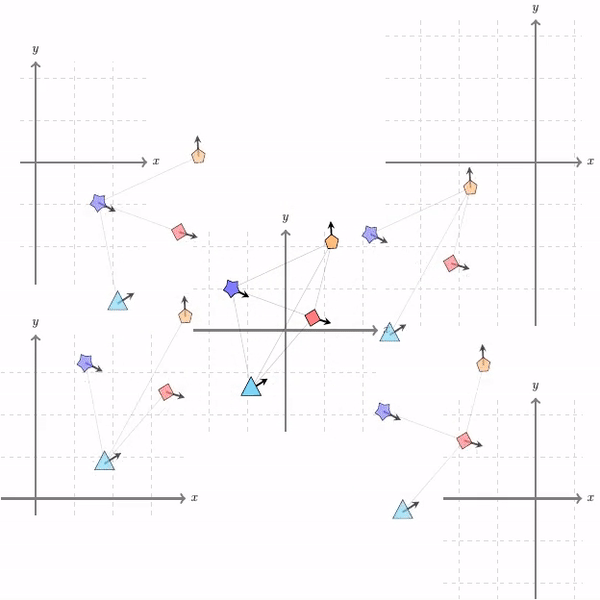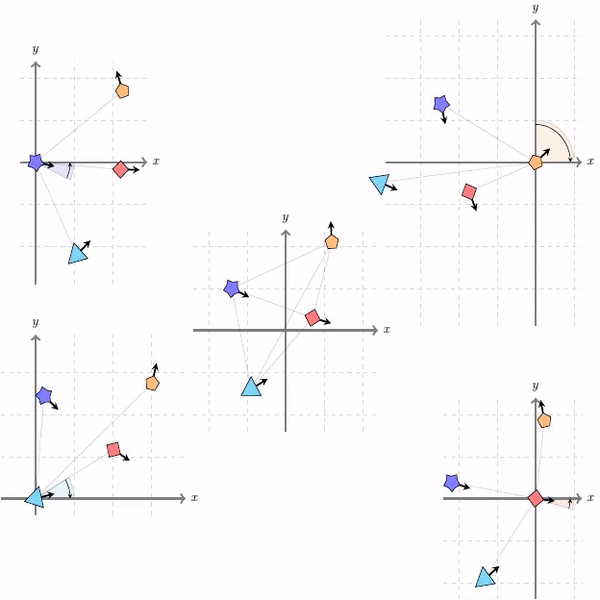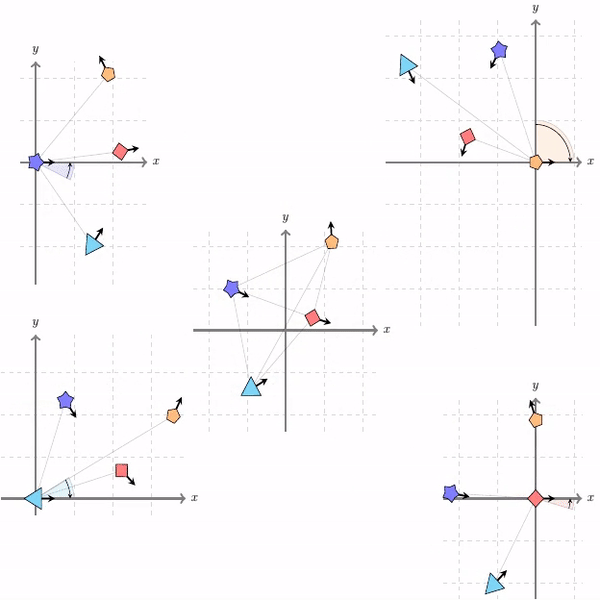 Roto-translated local coordinate frames
Roto-translated local coordinate frames
Abstract
Modelling interactions is critical in learning complex dynamical systems, namely systems of interacting objects with highly non-linear and time-dependent behaviour. A large class of such systems can be formalized as geometric graphs, i.e., graphs with nodes positioned in the Euclidean space given an arbitrarily chosen global coordinate system, for instance vehicles in a traffic scene. Notwithstanding the arbitrary global coordinate system, the governing dynamics of the respective dynamical systems are invariant to rotations and translations, also known as Galilean invariance. As ignoring these invariances leads to worse generalization, in this work we propose local coordinate frames per node-object to induce roto-translation invariance to the geometric graph of the interacting dynamical system. Further, the local coordinate frames allow for a natural definition of anisotropic filtering in graph neural networks. Experiments in traffic scenes, 3D motion capture, and colliding particles demonstrate that the proposed approach comfortably outperforms the recent state-of-the-art.
