Latent Field Discovery in Interacting Dynamical Systems with Neural Fields

Abstract

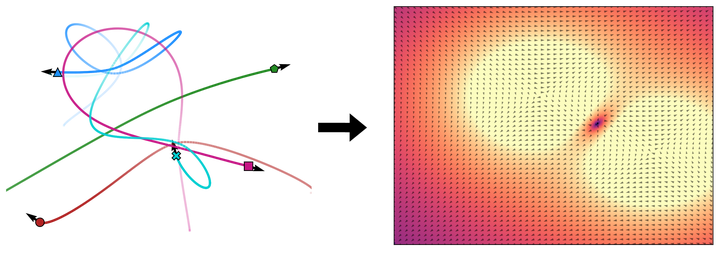
Systems of interacting objects often evolve under the influence of underlying field effects that govern their dynamics, yet previous works have abstracted away from such effects, and assume that systems evolve in a vacuum. In this work, we focus on discovering these fields, and infer them from the observed dynamics alone, without directly observing them. We theorize the presence of latent force fields, and propose neural fields to learn them. Since the observed dynamics constitute the net effect of local object interactions and global field effects, recently popularized equivariant networks are inapplicable, as they fail to capture global information. To address this, we propose to disentangle local object interactions –which are SE(3) equivariant and depend on relative states– from external global field effects –which depend on absolute states. We model the interactions with equivariant graph networks, and combine them with neural fields in a novel graph network that integrates field forces. Our experiments show that we can accurately discover the underlying fields in charged particles settings, traffic scenes, and gravitational n-body problems, and effectively use them to learn the system and forecast future trajectories.