 Amortized Equation Discovery in Hybrid Dynamical Systems
Amortized Equation Discovery in Hybrid Dynamical Systems
Abstract
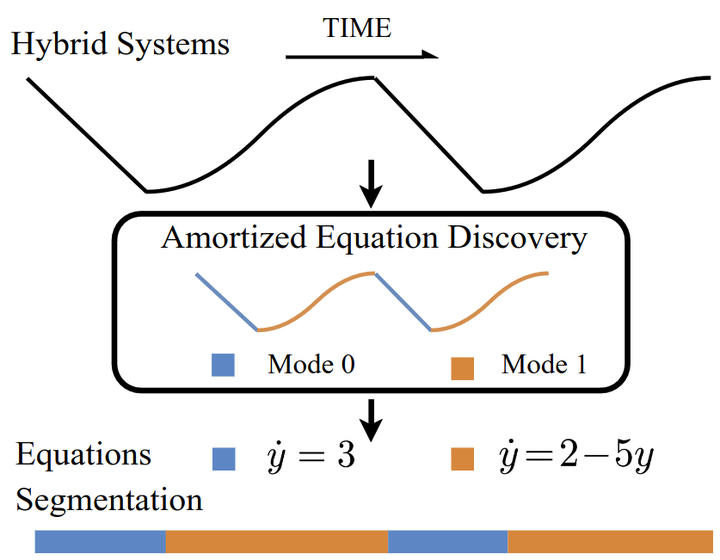
Hybrid dynamical systems are prevalent in science and engineering to express complex systems with continuous and discrete states. To learn the laws of systems, all previous methods for equation discovery in hybrid systems follow a two-stage paradigm, i.e. they first group time series into small cluster fragments and then discover equations in each fragment separately through methods in non-hybrid systems. Although effective, these methods do not fully take advantage of the commonalities in the shared dynamics of multiple fragments that are driven by the same equations. Besides, the two-stage paradigm breaks the interdependence between categorizing and representing dynamics that jointly form hybrid systems. In this paper, we reformulate the problem and propose an end-to-end learning framework, i.e. Amortized Equation Discovery (AMORE), to jointly categorize modes and discover equations characterizing the dynamics of each mode by all segments of the mode. Experiments on four hybrid and six non-hybrid systems show that our method outperforms previous methods on equation discovery, segmentation, and forecasting.